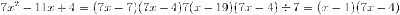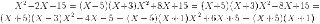sábado, 24 de octubre de 2009
jueves, 22 de octubre de 2009
sábado, 17 de octubre de 2009
Factor Común
Factorizar por factor común una expresión algebraica es representarla como un producto mediante el uso de una o varias veces de la propiedad distributuva de los números reales, que como ya sabemos es: xy + xz = x(y+z). Ver la Ley del Mosquetero
Ejemplo 1 . Factorizar
a) x2 — 9x = x(x—9)
b) 6x3y2 - 4x2y5 + 18xy6 = 2xy2 (3x2 — 2xy3 + 9y4)
c) 5x3 — lOx2 + 15x = 5x(x2 — 2x + 3)
Binomios con Término Semejante (ax+b)(cx+d) = acx2 + (ad + bc)x + bd
Este método se basa en el hecho de que si aplicamos dos veces la ley distributiva, ver Ley del Mosquetero al siquiente producto: (ax+b)(cx+d) obtenemos como resultado ac x2 + (ad + bc) x + bd
Para una forma más eficiente de su uso veamos el mismo resultado de la siguiente forma:
ac x2 + (ad + bc) x + bd
a b
c d
Al acomodar los factores adecuados abajo de la expresión, si multiplicamos en cruz: a por c y b por b vemos que su suma es el coeficiente de x, por lo que esto nos dá una herramienta directa para factorizar expresiones de esta forma.
Ejemplo 2
Factorizar 6 x2 + 13 x + 6
6 x2 + 13 x + 6
3 2
2 3
Vemos que colocando los factores de esta forma los productos cruzados son 9 y 4 y como la suma es 13 que es el término de enmedio el resultado es
(3x + 2) (2x + 3)
Vemos que acomodamos los términos de otra forma no obtenemos el resultado, por ejemplo si escribimos:
6 x2 + 13 x + 6
3 3
2 2
El resultado de la suma de los productos cruzados es 6 + 6 = 12 que no es el coeficiente del segundo término, por lo que el éxito de este método es el de probar y encontrar los factores adecuados, con los signos y el orden correcto.
Ejemplo 3:
Factorizar 5 x2 - 7 x - 6
5 x2 - 7 x - 6
5 +3
1 −2
Vemos que colocando los factores de 5 y de −6 de esta forma los productos cruzados son −10 y 3 y como la suma es −7 que es el término de enmedio el resultado es
(5x + 3) (x - 2)
Ejemplo 4:
Factorizar 9a2 — l2ab3 + 4b6
9a2 — l2ab3 + 4b6
3 −2
3 −2
a b3
a b3
Vemos que colocando los factores de 3 y de −2 de esta forma los productos cruzados son −6 y −6 y como la suma es −12 que es el término de enmedio el resultado es
(3a - 2b3)(3a - 2b3)
(3a - 2b3)2
Ejercicios:
a) 25 — x2
e) — x2 — x - 6
f) 6x2 + x —2
Trinomio cuadrado perfecto
Otra manera de ver el ejemplo anterior es considerarla como un trinomio cuadrado perfecto, esto es; el resultado de elevar al cuadrado un binomio. El primer término seria 3a y el segundo 2b3 , y el término de en medio es el doble de su producto, por lo que tenemos:
(3a - 2ab3)2
9a —l2ab +4b — (3a 2b
Agrupación
En muchas ocasiones no es posible factorizar una expresión dada por alguno do los métodos anteriores, sin embargo es posible agrupar los términos en dos partes, cada una de los cuales se puede factorizar por un método conocido; si después de separar y factorizar resultan términos con factor comón se puede aplicar el primer método, que viene siendo Ley del Mosquetero y la expresión inicial quedara factorizada.
Ejemplo 5 :
x3 — x2 +2x — 2
Factorizamos lo dos primeros términos y después los segundos
x2( x - 1) + 2(x — 1)
(x — 1)( x2 + 2)
Ejemplo 6 :
x3 +2x2 −3xy +y2 -y3
Agrupamos el primero y el ultimo término y después apliquemos el método
x3 -y3 +2x2 −3xy +y2
(x -y)(x2 +xy +y2 ) + (x —y)(2x —y)
(x —y)(x2 +xy+ y2 +2x -y)
Ejercicios:
a) ax -ay -bx +by
b) 20ac + 15bc +4ad + 3bd
c) 18a3 + 12a2 - 15a - 10
Productos notables
Como factorizar es basicamente lo contrarío de multiplicar, uno de los metódos más útiles en factorizaclón se obtiene al aplicar los [Productos Notables]], ya que son productos con los que el alumno está familiarizado.
Es importante señalar que si el alumno no domina los productos notables, este método en lugar de ser útil puede ser perjudicial, por lo que el alumno y el masetro deben de estar consientes de que sio no se tiene el tiempo suficiente para apreder y practicar los productos notables, es mejor no ver este método.
División Sintética o Regla de Ruffini:
Esta se utiliza cuando el divisor es de la forma * x – a* . Por medio de este procedimiento, se obtiene más fácilmente los Coeficientes en una división de polinomios. Aplicando
Se puede hallar el residuo, sin hallar la división: x2 – 7 x + 6 entre x – 5
Se sustituye la x por 5, y se obtiene: 52 – 7 (5) + 6 = 25 – 35 + 6 = – 4
• + 2 x + 7 entre x +3
Se sustituye la x por ( – 3), y se obtiene: - 3 3 + 2 ( −3 ) + 7 = −27 - 6 + 7 = −26
Aplicando la Regla de Ruffini para calcular los cocientes sin realizar la división:
Procedimiento: a. Se escribe todos los coeficientes del dividendo, y en la parte inferior izquierda,
sobre la horizontal se escribe 3 que aparece en el divisor, pero con signo
cambiado, para evitar la resta que se da en la división:
b. Los coeficientes del cociente se obtiene así:
El primero es igual al primer coeficiente del dividendo: 4 y se escribe debajo de
la línea
c. Los coeficientes se obtienen así:
El 12, es el producto de 3 x 4
El 24, es el producto de 3 x 8
El 78, es el producto de 3 x 26
El 234, es el producto de 3 x 78
Teorema del Residuo: Si un polinomio P ( x ) se divide entre x– r, el residuo es P ( r )2.7.3.2
Ejemplo: P ( x ) = 2x3 - 4x2 + 2x −1
a ) P ( 1 ) = 2 (1)3 - 4 (1)2 + 2 (1)x −1 = −1
b ) Luego usamos la división sintética para determinar el cociente y el residuo cuando P ( x ) = 2x3 - 4x2 + 2x −1 se divide entre x – 1
El procedimiento consiste en escribir únicamente los coeficientes, en orden de potenica descendiente; ponemos 0 si no hay término.
2 −4 2 −1 1
2 −2 0
--- --- --- ----
2 −2 0 −1
El cocientes es q(x) = 2x2 - 2x y el residuo en −1
Los resultados de la parte a) y de la parte b ) muestran que cuando P ( x) se divide entre x – 1, el residuo es P ( 1 ).
Teorema del Factor:2.7.3.3. Este Teorema nos explica cómo determinar un factor de un polinomio si el residuo de cierta división es cero.
Si P (x) = 0 si y sólo sí x – r es un factor de P( x )
Un cero de un polinomio en x, es todo valor de x que hace que el valor del polinomio sea igual a 0.
Ejemplo: Sea P (x) = x3 - 3x2 + 5x - 15
Demostremos que: a) P ( 3) = 0
Dividimos P(x) entre x −3 utilizando división sintética
1 −3 5 −15 3
3 0 15
--- --- --- ----
1 0 5 0
El residuo de esta división es 0.
De acuerdo con el Teorema del Residuo, éste es igual a P ( 3 )
Por lo tanto, P ( 3 ) = 0 y 3 es un cero del polinomio
b) x – 3 es un factor de P ( x ), el residuo es 0 y los números 1, y 5 de la división sintética en la parte a) representan los coeficientes del cociente, por lo que la factorización queda:
P (x) = x3 - 3x2 + 5x - 15 = (x - 3)(x2 + 5)
eq.latex
Factorizar por factor común una expresión algebraica es representarla como un producto mediante el uso de una o varias veces de la propiedad distributuva de los números reales, que como ya sabemos es: xy + xz = x(y+z). Ver la Ley del Mosquetero
Ejemplo 1 . Factorizar
a) x2 — 9x = x(x—9)
b) 6x3y2 - 4x2y5 + 18xy6 = 2xy2 (3x2 — 2xy3 + 9y4)
c) 5x3 — lOx2 + 15x = 5x(x2 — 2x + 3)
Binomios con Término Semejante (ax+b)(cx+d) = acx2 + (ad + bc)x + bd
Este método se basa en el hecho de que si aplicamos dos veces la ley distributiva, ver Ley del Mosquetero al siquiente producto: (ax+b)(cx+d) obtenemos como resultado ac x2 + (ad + bc) x + bd
Para una forma más eficiente de su uso veamos el mismo resultado de la siguiente forma:
ac x2 + (ad + bc) x + bd
a b
c d
Al acomodar los factores adecuados abajo de la expresión, si multiplicamos en cruz: a por c y b por b vemos que su suma es el coeficiente de x, por lo que esto nos dá una herramienta directa para factorizar expresiones de esta forma.
Ejemplo 2
Factorizar 6 x2 + 13 x + 6
6 x2 + 13 x + 6
3 2
2 3
Vemos que colocando los factores de esta forma los productos cruzados son 9 y 4 y como la suma es 13 que es el término de enmedio el resultado es
(3x + 2) (2x + 3)
Vemos que acomodamos los términos de otra forma no obtenemos el resultado, por ejemplo si escribimos:
6 x2 + 13 x + 6
3 3
2 2
El resultado de la suma de los productos cruzados es 6 + 6 = 12 que no es el coeficiente del segundo término, por lo que el éxito de este método es el de probar y encontrar los factores adecuados, con los signos y el orden correcto.
Ejemplo 3:
Factorizar 5 x2 - 7 x - 6
5 x2 - 7 x - 6
5 +3
1 −2
Vemos que colocando los factores de 5 y de −6 de esta forma los productos cruzados son −10 y 3 y como la suma es −7 que es el término de enmedio el resultado es
(5x + 3) (x - 2)
Ejemplo 4:
Factorizar 9a2 — l2ab3 + 4b6
9a2 — l2ab3 + 4b6
3 −2
3 −2
a b3
a b3
Vemos que colocando los factores de 3 y de −2 de esta forma los productos cruzados son −6 y −6 y como la suma es −12 que es el término de enmedio el resultado es
(3a - 2b3)(3a - 2b3)
(3a - 2b3)2
Ejercicios:
a) 25 — x2
e) — x2 — x - 6
f) 6x2 + x —2
Trinomio cuadrado perfecto
Otra manera de ver el ejemplo anterior es considerarla como un trinomio cuadrado perfecto, esto es; el resultado de elevar al cuadrado un binomio. El primer término seria 3a y el segundo 2b3 , y el término de en medio es el doble de su producto, por lo que tenemos:
(3a - 2ab3)2
9a —l2ab +4b — (3a 2b
Agrupación
En muchas ocasiones no es posible factorizar una expresión dada por alguno do los métodos anteriores, sin embargo es posible agrupar los términos en dos partes, cada una de los cuales se puede factorizar por un método conocido; si después de separar y factorizar resultan términos con factor comón se puede aplicar el primer método, que viene siendo Ley del Mosquetero y la expresión inicial quedara factorizada.
Ejemplo 5 :
x3 — x2 +2x — 2
Factorizamos lo dos primeros términos y después los segundos
x2( x - 1) + 2(x — 1)
(x — 1)( x2 + 2)
Ejemplo 6 :
x3 +2x2 −3xy +y2 -y3
Agrupamos el primero y el ultimo término y después apliquemos el método
x3 -y3 +2x2 −3xy +y2
(x -y)(x2 +xy +y2 ) + (x —y)(2x —y)
(x —y)(x2 +xy+ y2 +2x -y)
Ejercicios:
a) ax -ay -bx +by
b) 20ac + 15bc +4ad + 3bd
c) 18a3 + 12a2 - 15a - 10
Productos notables
Como factorizar es basicamente lo contrarío de multiplicar, uno de los metódos más útiles en factorizaclón se obtiene al aplicar los [Productos Notables]], ya que son productos con los que el alumno está familiarizado.
Es importante señalar que si el alumno no domina los productos notables, este método en lugar de ser útil puede ser perjudicial, por lo que el alumno y el masetro deben de estar consientes de que sio no se tiene el tiempo suficiente para apreder y practicar los productos notables, es mejor no ver este método.
División Sintética o Regla de Ruffini:
Esta se utiliza cuando el divisor es de la forma * x – a* . Por medio de este procedimiento, se obtiene más fácilmente los Coeficientes en una división de polinomios. Aplicando
Se puede hallar el residuo, sin hallar la división: x2 – 7 x + 6 entre x – 5
Se sustituye la x por 5, y se obtiene: 52 – 7 (5) + 6 = 25 – 35 + 6 = – 4
• + 2 x + 7 entre x +3
Se sustituye la x por ( – 3), y se obtiene: - 3 3 + 2 ( −3 ) + 7 = −27 - 6 + 7 = −26
Aplicando la Regla de Ruffini para calcular los cocientes sin realizar la división:
Procedimiento: a. Se escribe todos los coeficientes del dividendo, y en la parte inferior izquierda,
sobre la horizontal se escribe 3 que aparece en el divisor, pero con signo
cambiado, para evitar la resta que se da en la división:
b. Los coeficientes del cociente se obtiene así:
El primero es igual al primer coeficiente del dividendo: 4 y se escribe debajo de
la línea
c. Los coeficientes se obtienen así:
El 12, es el producto de 3 x 4
El 24, es el producto de 3 x 8
El 78, es el producto de 3 x 26
El 234, es el producto de 3 x 78
Teorema del Residuo: Si un polinomio P ( x ) se divide entre x– r, el residuo es P ( r )2.7.3.2
Ejemplo: P ( x ) = 2x3 - 4x2 + 2x −1
a ) P ( 1 ) = 2 (1)3 - 4 (1)2 + 2 (1)x −1 = −1
b ) Luego usamos la división sintética para determinar el cociente y el residuo cuando P ( x ) = 2x3 - 4x2 + 2x −1 se divide entre x – 1
El procedimiento consiste en escribir únicamente los coeficientes, en orden de potenica descendiente; ponemos 0 si no hay término.
2 −4 2 −1 1
2 −2 0
--- --- --- ----
2 −2 0 −1
El cocientes es q(x) = 2x2 - 2x y el residuo en −1
Los resultados de la parte a) y de la parte b ) muestran que cuando P ( x) se divide entre x – 1, el residuo es P ( 1 ).
Teorema del Factor:2.7.3.3. Este Teorema nos explica cómo determinar un factor de un polinomio si el residuo de cierta división es cero.
Si P (x) = 0 si y sólo sí x – r es un factor de P( x )
Un cero de un polinomio en x, es todo valor de x que hace que el valor del polinomio sea igual a 0.
Ejemplo: Sea P (x) = x3 - 3x2 + 5x - 15
Demostremos que: a) P ( 3) = 0
Dividimos P(x) entre x −3 utilizando división sintética
1 −3 5 −15 3
3 0 15
--- --- --- ----
1 0 5 0
El residuo de esta división es 0.
De acuerdo con el Teorema del Residuo, éste es igual a P ( 3 )
Por lo tanto, P ( 3 ) = 0 y 3 es un cero del polinomio
b) x – 3 es un factor de P ( x ), el residuo es 0 y los números 1, y 5 de la división sintética en la parte a) representan los coeficientes del cociente, por lo que la factorización queda:
P (x) = x3 - 3x2 + 5x - 15 = (x - 3)(x2 + 5)
eq.latex
jueves, 15 de octubre de 2009
TEMARIO
1.- COMPETENCIAS DE CURSO DE MATEMATICAS.
2.- ESTAR DISPUESTOS A ENFRENTAR RETOS MATEMATICOS.
3.- UTILIZAR ADECUADAMENTE LOS NUMEROS REALES.
4.- REALIZAR OPERACIONES CON FRACCIONES.
5.- FACTORIZAR EXPRESIONES AIGEBRAICAS.
6.- UTILIZAR ADECUADAMENTE LA SINTAXIS Y LA SEMANTICA DE LAS EXPRESIONES AIGEBRAICAS.
7.- JUSTIFICAR LOS PROCEDIMIENTOS.
8.- APLICAR EL TEOREMA DE PITAGORAS.
9.- APLICAR EL CALCULO TRIGONOMETRICO.
10.- UTILIZAR LAS PROPIEDADES DE LA IGUALDAD PARA RESOLVER ECUACIONES.
1.- COMPETENCIAS DE CURSO DE MATEMATICAS.
2.- ESTAR DISPUESTOS A ENFRENTAR RETOS MATEMATICOS.
3.- UTILIZAR ADECUADAMENTE LOS NUMEROS REALES.
4.- REALIZAR OPERACIONES CON FRACCIONES.
5.- FACTORIZAR EXPRESIONES AIGEBRAICAS.
6.- UTILIZAR ADECUADAMENTE LA SINTAXIS Y LA SEMANTICA DE LAS EXPRESIONES AIGEBRAICAS.
7.- JUSTIFICAR LOS PROCEDIMIENTOS.
8.- APLICAR EL TEOREMA DE PITAGORAS.
9.- APLICAR EL CALCULO TRIGONOMETRICO.
10.- UTILIZAR LAS PROPIEDADES DE LA IGUALDAD PARA RESOLVER ECUACIONES.
Suscribirse a:
Entradas (Atom)

+de+eq+6.gif)
+de+eq+6.gif)